线段CF的最大值如何计算？

在线性代数和几何学中，线段的长度是一个基础且重要的概念。当我们谈论线段CF的最大值计算时，实际上是在讨论在给定条件约束下，如何求得特定线段的最大长度。这一问题可能出现在多个数学领域中，如平面几何、向量空间或是优化问题。本文将全面指导您如何计算线段CF的最大值，以及提供相关问题的解决方案。

理解线段的定义

我们需要明确什么是线段。在几何学中，线段是由两点之间最短路径所定义的几何对象。点C和点F确定了一条线段CF。计算线段长度的最直接方法是使用距离公式：如果点C的坐标为(x1,y1)，点F的坐标为(x2,y2)，那么线段CF的长度可以通过以下公式计算：

\[\text{线段CF的长度}=\sqrt{(x2-x1)^2+(y2-y1)^2}\]

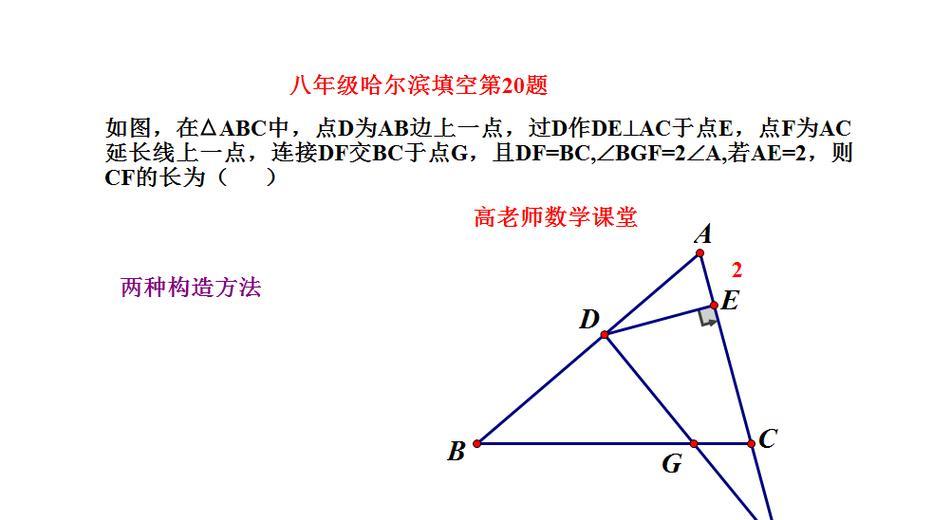
线段CF最大值的计算方法

在实际问题中，线段CF的最大值可能受到一些特定条件的约束。这些条件可能是几何条件（如点C和F位于特定的几何形状内）、代数条件（如点C和F的坐标满足某些方程）或是其他类型的问题约束。要计算线段CF的最大值，一般的方法包括：

方法1：几何法

当问题具有几何性质时，可以通过作图和观察来找到线段长度的最大值。如果点C和点F位于圆周上，我们可以利用圆的对称性质和直角三角形的性质来求解。

方法2：代数法

对于代数条件限制下的线段长度问题，我们通常需要通过建立函数关系，然后利用求导数找到极值点的方法来求解。对于线段CF的长度，我们可以将其表示为关于某个变量的函数，并求解该函数的最大值。

方法3：优化算法

在更复杂的问题中，可能需要运用数值优化算法来逼近线段CF的最大值。我们可以利用梯度下降法、遗传算法等高级技术来解决线段长度的最优化问题。

计算线段CF最大值的步骤

1.问题分析：确定问题的条件和约束，明确线段CF的定义。

2.建立函数：根据问题条件，建立表示线段CF长度的函数表达式。

3.求导求极值：对函数进行求导，找到可能的极值点。

4.边界条件检验：分析边界条件是否可能产生最大值。

5.验证结果：检验所得的极值是否为最大值，并考虑特殊情况。

常见问题与实用技巧

常见问题

如果线段CF位于一个动态变化的几何图形内，如何保证计算的准确性？

在多维空间中，如何求解线段CF的最大值？

实用技巧

在复杂几何问题中，绘制准确的示意图能极大地帮助我们理解和分析问题。

使用计算机代数系统（如Mathematica或MATLAB）可以帮助我们处理复杂的代数计算。

对于多维空间的问题，可以将问题转化为线性规划问题，并使用线性规划的算法进行求解。

结语

在求解线段CF的最大值问题时，关键在于准确地建立数学模型并应用合适的数学工具。通过上述方法和步骤的介绍，我们能更加有效地分析和解决问题。无论是在学术研究还是实际应用中，这些技巧和策略都是求解线段最大长度问题的有力工具。综合以上内容，我们已经全面了解了如何在各种条件下计算线段CF的最大值，希望这些知识能够帮助您在相关领域取得进展。